
plot ( x, - f ( x ), label = "Reflection of $y = \log_2(x)$", color = "red", sketch_params = 0.8 ) pts = fmts = for i in range ( 0, len ( pts )) : plt. axvline ( color = "black", linewidth = 1 ) plt.
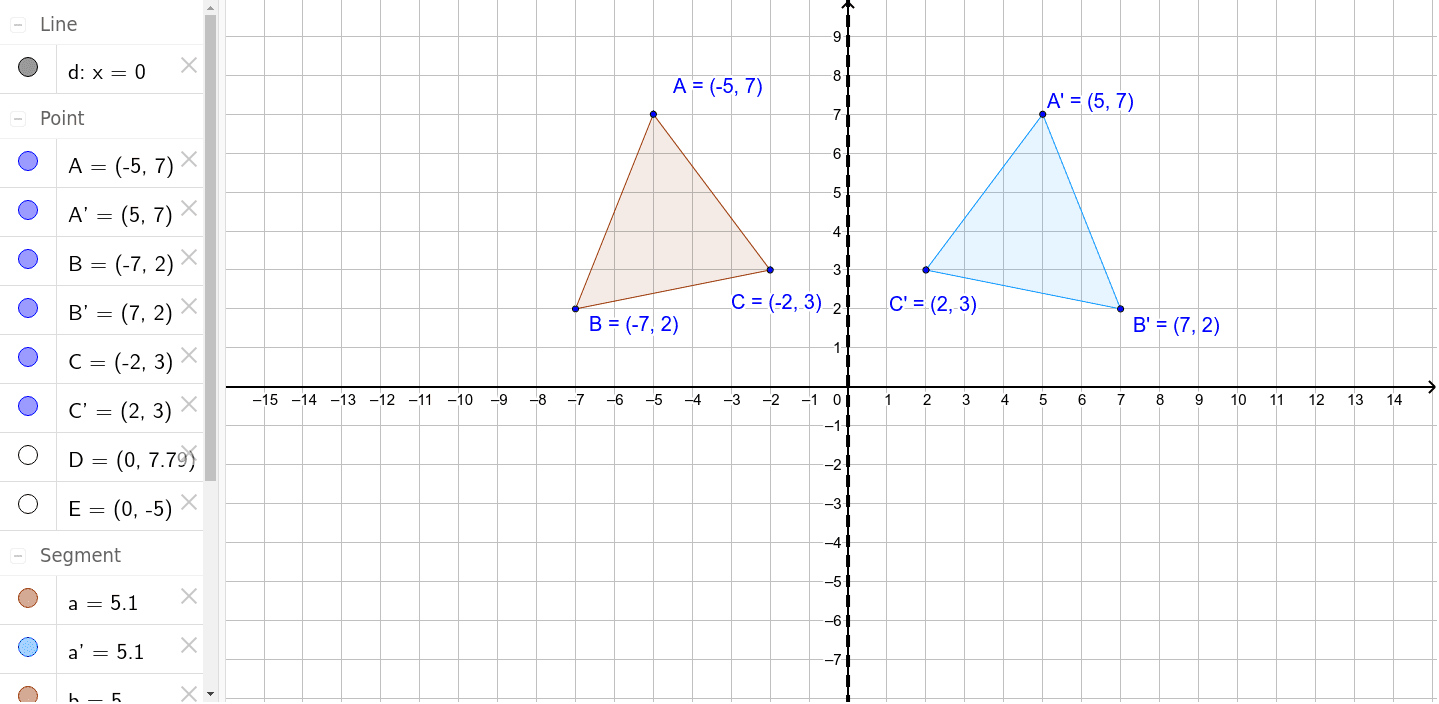
axhline ( color = "black", linewidth = 1 ) plt. vectorize ( g ) xmin, xmax = 0.01, 10 nsamples = 100 #2*(xmax - xmin) - 1 x = np. Import matplotlib import numpy as np import matplotlib.pyplot as plt from math import log def draw (): def g ( x ): return log ( x, 2 ) f = np. We start by identifying a few points on the graph of \(y = \log_2(x)\). (Even computer programs that graph functions typically just plot a bunch of points and connect them by straight lines, but they plot so many points that it looks accurate.)Įxample: Let’s reflect the graph of \(y = \log_2(x)\) across the \(x\)-axis. Usually, it will suffice to sample and reflect a few points and connect the dots with a curve. Or more accurately, if we had the time to sample and reflect infinitely many points, we would get the reflection of the graph. This is the reflection of the graph across the \(x\)-axis. If we only reflect a few points, the red dots don’t look like much,īut as we reflect more and more points, the red dots start to resemble the blue curve but flipped upside-down. If we have a point on the \(x\)-axis and we reflect it across the \(x\)-axis, we get the same point back. Then \(P'\) has the same \(x\)-coordinate as \(P\), but its \(y\)-coordinate is the negative of \(P\)’s.Įxample: Suppose we have instead the point \(P = (2, 0)\). Rule: For an arbitrary point \((x, y)\), its reflection across the \(x\)-axis is the point \((x, -y)\).Įxample: Consider the point \(P = (1, 3)\). Putting these two facts together, we get the following rule: (so one is positive and the other negative, unless the points are on the \(x\)-axis)Īnd the fact that the two points are equally distant from the \(x\)-axis. This follows from the fact that the two points are on opposite sides of the \(x\)-axis More generally, if a point has a \(y\)-coordinate of \(a\), its reflection has the \(y\)-coordinate \(-a\). Its reflection has the \(y\)-coordinate -17. What is meant by that is if a point has a \(y\)-coordinate of, say, 17, Which means the points are directly above one another, so they have the same \(x\)-coordinate.Ī point and its reflection across the \(x\)-axis have equal but opposite \(y\)-coordinates. This line from point to point has to be perfectly vertical, Since the \(x\)-axis is perfectly horizontal, Has to intersect the \(x\)-axis at a right angle. This is because the line from a point to its reflection across the \(x\)-axis If you were able to solve the exercise, you might already have guessed the following facts:Ī point and its reflection across the \(x\)-axis have the same \(x\)-coordinate.

Transformations of Objects and Shapes: Exercises Transformations: Positions and Motions of Objects and Shapes Rates, Ratios, and Proportional Reasoning Inductive Reasoning and Deductive Reasoning Or visit the Store to make a Task Tracker purchase.Ī light ray approaches a mirror at an angle of incidence of 25°.Approximating Square Roots of Non-Perfect SquaresĬreating, Labelling, and Interpreting Line Graphs Return to the Main Page to link into Version 2. They can modify our pre-made problem sets, write their own problems with our easy-to-use Problem Builder, and use the Calculator Pad to design their own program that expresses their emphasis on the use of mathematics in Physics.
REFLECTION GRAPH PROBLEMS FREE
While the FREE version does all the above, teachers with a Task Tracker subscription can take things a step further. And we've maintained the same commitment to providing help via links to existing resources. Student answers are automatically evaluated and feedback is instant.

REFLECTION GRAPH PROBLEMS GENERATOR
Version 2 is now LIVE! We have more than tripled the number of problems, broken each unit into several smaller, single-topic problem sets, and utilized a random number generator to provide numerical information for each problem. We have recently revised and improved The Calculator Pad.

You are viewing the Legacy Version of The Calculator Pad.


 0 kommentar(er)
0 kommentar(er)
